更新人工经济模型的基本规则

首先回顾一下人工经济模型的基本交易规则：

  1. 经济系统中人和财富的总量保持不变；
  2. 开始的时候，每个人都有等量的货币；
  3. 每当两个主体相遇，他们就随机分配财富。

这样的经济系统非常野蛮、非常不合理，现实世界中并不是这样做交易的，通常你不会把自己的钱花光，而是会留存一定比例，然后把剩下的钱用于交易，因此我们可以考虑引入一个非常重要的变量——储蓄率，每个主体都有自己的储蓄率，它是一个(0, 1)之间的小数。每个人在交易的时候，会保留储蓄率乘以自己财富总量的财富，剩余财富用于交易，并且交易仍然是随机的。更新后的人工经济模型的交易规则变为：

  1. 经济系统中人和财富的总量保持不变；
  2. 开始的时候，每个人都有等量的货币；
  3. 每个主体有自己的储蓄率；
  4. 每当两个主体相遇，他们会将除储蓄部分外的财富用于随机分配。

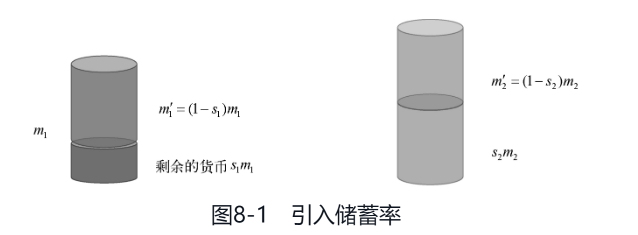
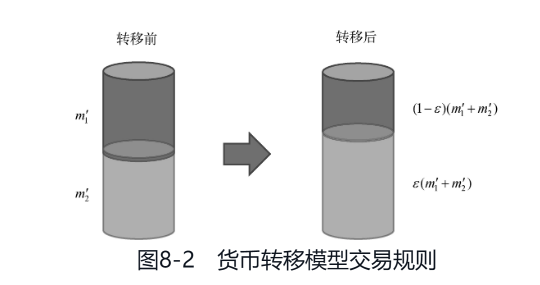
image.png

image.png

程序修改

接下来看看如何用程序实现新的经济模型规则。首先引入储蓄率，增加一个turtles-own的变量——save_rate，因为每一个主体的储蓄率都不一样，所以要把它放在turtles-own的变量中。在有多个变量的情况下，用回车隔开不同变量，并且都放在方括号内。

1
2
3
4
turtles-own [
    money
    save_rate
]

接下来初始化的时候，要初始化save_rate的具体数值，我们在创建一个主体的时候，用random-float设定它的储蓄率是一个0~1之间的随机数：

1
2
3
4
5
6
7
8
9
to setup
    clear-all
    reset-ticks
    create-turtles num_agents [
        set money (total_money / num_agents)
        setxy random-xcor random-ycor
        set save_rate random-float 1
    ]
end

而且这个数值一旦定下来将不再变化，道理很简单，因为每个人的储蓄率基本上是固定的。储蓄率越高，表示这个交易者比较保守，因为他只拿一小部分钱用于交易；反过来，储蓄率越低，表示交易者更偏向于冒险，他会用更多的钱来进行交易。
接下来，添加一个全新的“new_go”按钮，方便比较两套交易规则，to go代码完全保留，而把全新的交易规则放在to new_go代码块中，这两个按钮都带持续循环标志

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
to new_go
    ask turtles[
        let agsets other turtles
        if count agsets >= 1
        [
            transaction_new (one-of agsets)
        ]
        forward 1
    ]
    tick
end

to transaction_new [trader]
    let deltam 0
    let money0 ((1 - save_rate) * money)
    let money1 ((1 - ([save_rate] of trader)) * ([money] of trader))
    let epsilon (random-float 1)
    set deltam (epsilon - 1) * money0 + epsilon * money1

    if money + deltam >= 0 and ([money] of trader) - deltam >= 0
    [
        set money money + deltam
        ask trader[
            set money money - deltam
        ]

    ]
end

两种规则下的财富分布对比

执行go命令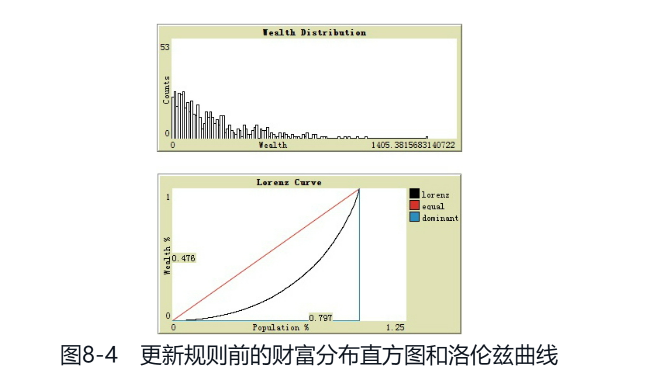
image.png
执行new_go命令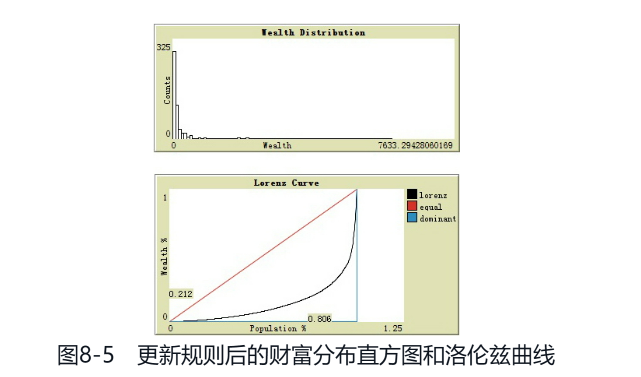
image.png

基尼系数的定义及程序实现

目前来看，这套全新的规则比较成功，能够复现我们感兴趣的现象。为了更加合理地刻画社会财富分布的不均衡性，也为了进一步比较不同的模型、不同的参数如何影响交易的不均衡性，我们引入一个全新的指标——基尼系数。

什么是基尼系数

基尼系数是国际通用的衡量一个经济体社会财富分布不均衡性的指标。基尼系数不仅能够用于衡量社会财富分布，也可以衡量更多其他量分布的不均衡性，比如衡量社交媒体上不同人粉丝数分布的不均衡性。

基尼系数的计算方法

第7章讲到洛伦兹曲线如果越弯曲越靠近折线，那么社会财富分布就越不均衡，因此我们不妨用洛伦兹曲线和对角线所围成的曲边三角形的面积来衡量社会财富分布的不均衡性，如图8-6所示。这个面积如果计算出来是S的话，那么最终G = 2S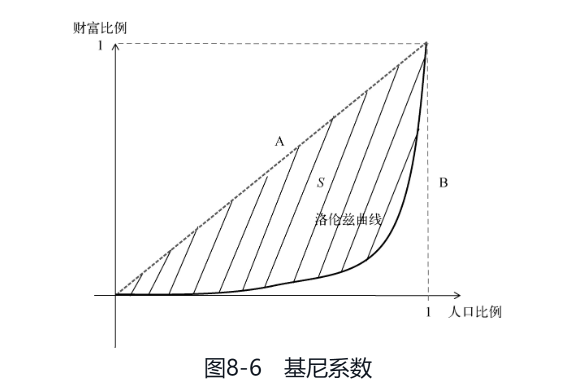
image.png

基尼系数的程序实现

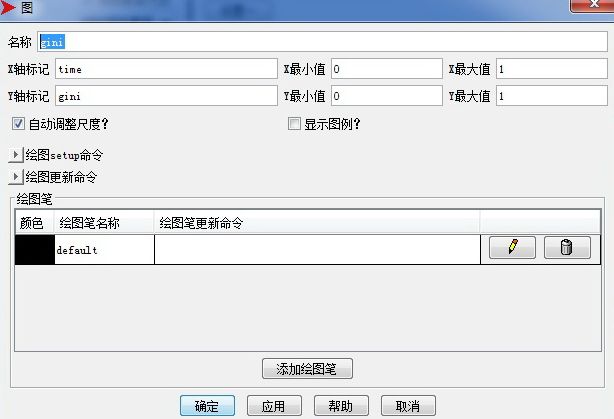
image.png
设置名称为gini，横坐标是time，我们可以看到每一时刻基尼系数的大小，纵坐标就是基尼系数本身。这里面不修改绘图笔指令，具体绘制基尼系数的命令将在代码里完成。如何在计算机中计算这样一个洛伦兹曲线和对角线所围成的曲边三角形的面积？我们可以用数值积分的方法。具体思想是，对这个曲边三角形进行矩形刨分，把整个[0, 1]区间分成若干份，实际上有多少人口就划分成多少份。然后计算每一个小矩形的面积，再把所有小矩形的面积累加起来，就可以近似得到曲边三角形的面积，如图8-8所示。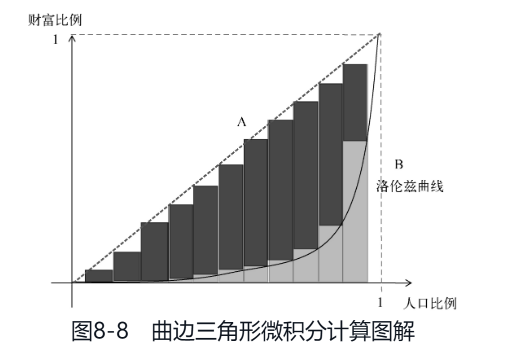
image.png
具体来讲，比如第i个小矩形的面积如何计算呢？首先可以计算每一个小矩形的宽度，我们把[0, 1]这个区间划分成num_agents份，因此每一份的宽度是1 / num_agents。小矩形的高度是：
i / num_agents - wealth-sum-so-far / total_wealth
这里i / num_agents是对角线在该点的纵坐标，wealth-sum-so-far / total_wealth是洛伦兹曲线在该点的纵坐标。于是可以用“宽×高”计算出这个小矩形的面积。如此计算出所有矩形的面积，再把它们累加起来就得到了曲边三角形的面积。接下来看看如何编写代码。为了计算基尼系数，我们只要改动绘制洛伦兹曲线的这部分代码即可，前面都一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
to update-lorenz-plot
    ;绘制财富分布绝对均衡的曲线
    clear-plot
    set-current-plot-pen "equal"
    plot 0
    plot 1

    ;绘制财富分布极端不均衡的曲线
    set-current-plot-pen "dominant"

    plot-pen-down
    plotxy 0 0
    plotxy 1 0
    plotxy 1 1
    plot-pen-up

    ;绘制洛伦兹曲线
    set-current-plot-pen "lorenz"
    set-plot-pen-interval 1 / num_agents
    plot 0

    let sorted-wealths sort [money] of turtles
    let total-wealth sum sorted-wealths
    let wealth-sum-so-far 0
    let index 0
    let gini 0

    repeat num_agents [
        set wealth-sum-so-far (wealth-sum-so-far + item index sorted-wealths)
        plot (wealth-sum-so-far / total-wealth)
        set index (index + 1)
        set gini gini + ((index / num_agents) - (wealth-sum-so-far / total-wealth)) / num_agents
    ]

    set-current-plot "gini" ;;指定绘画gini图
    plot gini * 2 ;; 一个时间点得到一个基尼系数
end

image.png
基尼系数表明，新规则造成的社会财富分布不均衡要比旧规则更严重。

使用行为空间做重复实验

接下来系统地探索参数是如何影响基尼系数的。这里介绍一个全新的工具——行为空间（BehaviorSpace），它可以让你通过简单的参数设置，自动实现同时进行大量重复的计算机模拟实验，并将实验结果自动记录到一个数据库文件中，方便我们探索不同的模型参数组合。在NetLogo的菜单栏中找到“工具”菜单，然后选择“行为空间”项。我们将会看到图8-14所示的界面，单击“新建”，就可以开始一系列实验。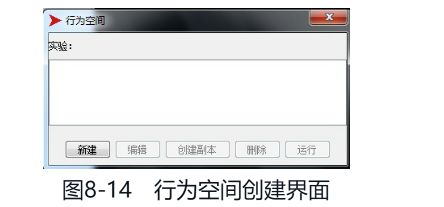
image.png
在行为空间设置界面，首先将这个实验命名为gini-experiment，如图8-15所示。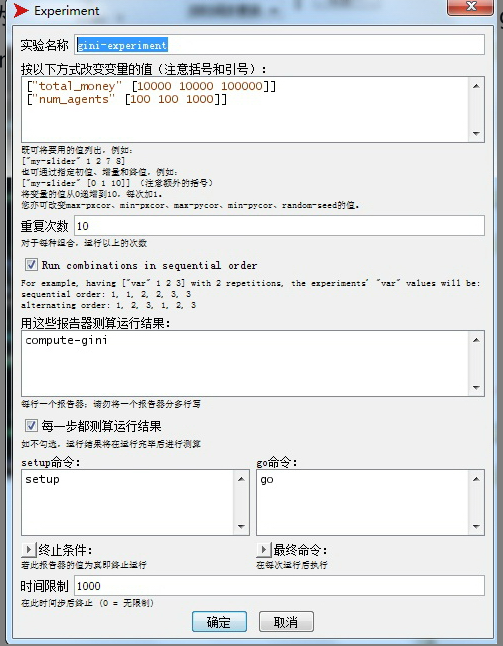
image.png
接下来指定参数变化的范围。我们希望探索的是，当num_agents等于100、200、300、……一直到1000，total_money等于10 000、20 000、30 000、……一直到100000，不同参数组合下的基尼系数。
image.png
每一个组合下都要进行重复实验。因为实验是随机性的，所以每一次计算出来的基尼系数都会有一定的波动。为了消除这种噪声影响，需要进行重复实验。这里设置每一个参数组合下重复10次，因此一共要做1000次实验。
接下来我们用这些报告测算运行结果，即每一种参数组合下的实验会有什么样的输出结果，这里不可能用动画或者图形作为输出，通常要计算并输出一些数值，对于本例就是基尼系数。
因此在“用这些报告器测算运行结果：”下输入一个自定义的函数——compute-gini。也就是当有一组参数值设定时，它就动态激活compute-gini代码去做模拟实验。
最后需要设定它的终止条件，这里只要设定最大模拟周期为1000即可。这样就定义好了一个行为空间，接下来给出compute-gini代码的写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
to-report compute-gini
    let sorted-wealths sort [money] of turtles
    let total-wealth sum sorted-wealths
    let wealth-sum-so-far 0
    let index 0
    let gini 0

    repeat num_agents [
        set wealth-sum-so-far (wealth-sum-so-far + item index sorted-wealths)
        plot (wealth-sum-so-far / total-wealth)
        set index (index + 1)
        set gini gini + ((index / num_agents) - (wealth-sum-so-far / total-wealth)) / num_agents
    ]

    set-current-plot "gini"
    report gini * 2
end

实际上，它就是把前面计算基尼系数的代码复制过来了，不同之处在于它不是to和end，而是to-report和end，report的意思是最终要有返回结果，即最终基尼系数要作为这个函数的结果输出。
写完代码以后，这个实验就可以运行了。单击运行，设置一下运行选项，如图8-16所示。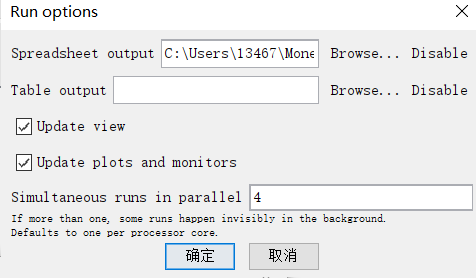
image.png
如果出现报错：没有选中的绘图。请使用set-current-plot指令选择绘图. 则要在更新洛伦兹的函数里指明set-current-plot "Lorenz curve"
模拟结果：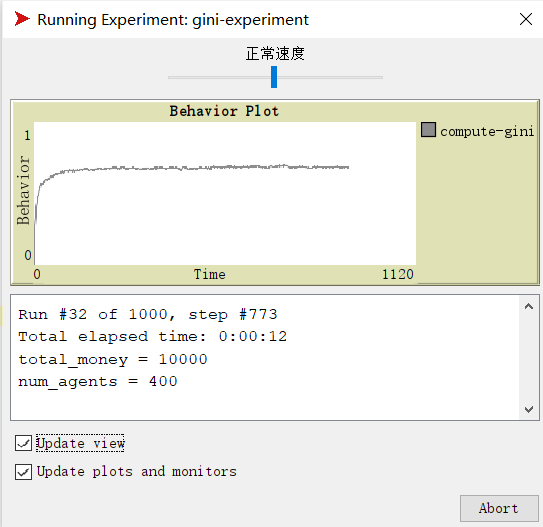
image.png
这个表单包括实验的名称、时间以及关键参数、多次模拟实验结果，并且记录了每一次模拟实验的参数取值、total_money取值、num_agents取值、最后的模拟步数以及基尼系数的运行结果。[final]这一行就是基尼系数的运行结果，因为这组结果是重复3次实验得到的，所以我们只需要把这3次的基尼系数求平均就可以得到参数组合下的基尼系数。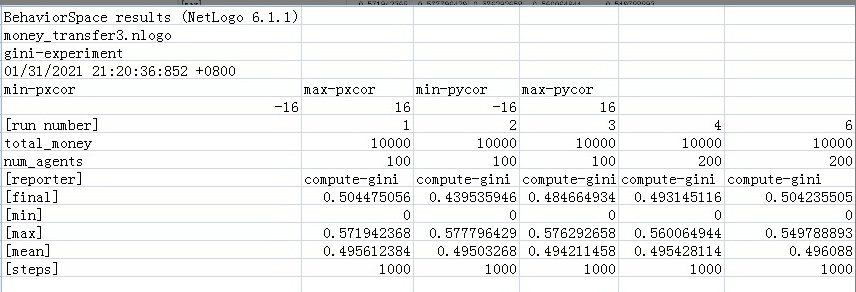image.png
最后可以绘制一个曲面，x坐标和y坐标分别对应total_money和num_agents，而[坐标对应基尼系数。这样我们就对模型的性质有了更深刻的了解。

小结

本章首先更新了交易规则，然后讲解了如何计算基尼系数，以及如何用NetLogo实现简单的数值积分以计算基尼系数，最后介绍了行为空间，以及如何用行为空间做重复性实验。