本章将介绍一个全新的人工生命模型——朗顿的蚂蚁。

4.1 朗顿的蚂蚁

image.png
我们会看到一只小蚂蚁在模拟世界里爬来爬去，神奇之处在于，模型运行时间足够长的话，这只蚂蚁会产生令人惊喜的行为，它会在模拟世界中修建出一条“高速公路”，而且这一现象是不依赖于初始条件的，如图4-1所示。通过这个人工生命的简单例子，我们还将介绍如何实现turtle与patch之间的互动。
image.png

  1. 规则一：如果当前这只蚂蚁所处的方格是白色的，则蚂蚁向右侧旋转90度，将方格涂成黑色，并且往前移动一格
  2. 规则二：如果当前这只蚂蚁所处的方格是黑色的，则蚂蚁向左侧旋转90度，将方格涂成白色，并且往前移动一格

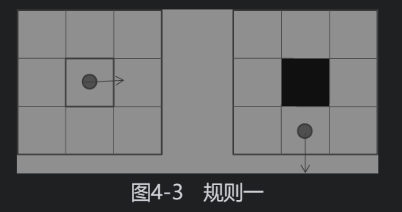
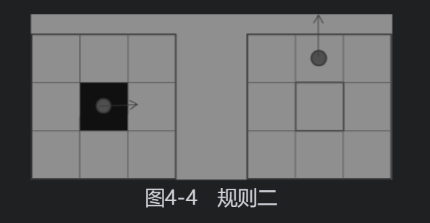
image.png

image.png

4.2 创建蚂蚁

  1. heading是turtle的一个属性
  2. netlogo字典中有turtle的相关属性和方法
    1
    2
    3
    4
    5
    6
    to setup
        clear-all
        create-turtles 1 [
            set heading random 3 * 90
        ]
    end

random命令

random x。
x是一个整数，
如果x>0, random x产生一个介于0和x之间的随机数
如果x<0,random x产生一个介于x和0之间的随机数。
第3章提到了一个命令random-float，这里random x产生的随机数一定是整数，这是它和random-float最大的不同。
接下来具体解读set heading random 3 * 90这条语句。
大家可能会把它解读成设置turtle的朝向为在0度到270度之间随机取一个整数，它可以取30度、60度，也可以取90度。但其实并非如此，之所以大家会理解有误，主要原因在于不熟悉NetLogo的语法。
random命令后面的数字3是作为random这个函数的参数来调用的，它会先从0、1、2、3这4个数字里随机取一个整数，然后把数值乘以90。因此heading的取值只能有4种可能，分别是0、90、180、270。也就是说，这条语句相当于:
set heading = (random 3) * 90

4.3 让蚂蚁动起来

  1. right x是让蚂蚁向右转动x度 = left (-x)
  2. left x是让蚂蚁向左转动x度
  3. 一个turtle对应于一个patch，但是一个patch可以对应多个turtle。如果要获得所有的turtle，使用turtles-here命令。所以在遍历turtles时，由于关系的对应，可以获得特定的patch的相关属性
  4. 使用tick计时
    1. tick来源于英文单词tick，这是一个象声词（“嘀嗒”），就像跑步比赛用秒表来计时一样，一开跑就按下秒表开始计时。
    2. 在setup代码中添加reset-ticks，也就是在每一次初始化时，重置秒表，然后在togo代码块中添加tick，表示每一个模拟周期计数一次。
  5. 如果按下“go”按钮，它并不是一步一步运行的，原因是“视图更新方式”设置了“连续更新”，这里换成“按时间步更新”。现在运行就是一步一步显示了。
1
2
3
4
5
6
7
8
9
10
11
12
13
to go
    ask turtles[
        ifelse (pcolor = white)[
            right 90
            set pcolor black
            forward 1
        ][
            left 90
            set pcolor white
            forward 1
        ]
    ]
end

4.4 小结

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

to setup
  clear-all // 清除页面中的所有元素
  reset-ticks // 重新设定计时器
  create-turtles 1[ // 创造 1 个turtle
  set heading (random 3) * 90  
    // set heading random 3 * 90 两者是等价的
  ]

end

to go
  ask turtles[
    ifelse (pcolor = white)[
      right 90
      set pcolor black
    ][
      left 90
      set pcolor white
    ]
    forward 1
  ]
  tick
end

那为什么这只蚂蚁要在走一万多步以后才开始修建“高速公路”呢?
谁也不知道答案，包括朗顿自己。后来很多科学家想通过数学分析的方式给出答案。在不同的条件下是否会产生不同的轨道?我们反复不停地随机初始化它的条件，发现它在一万多步的时候总是会修建出这样的“高速公路”，尽管每次“高速公路”的朝向以及它起始的时间可能会不太一样，但是修建“高速公路”似乎是朗顿的蚂蚁模拟程序的一个吸引子一样。为什么朗顿的蚂蚁会修建这样一条“高速公路”仍然是一个谜，这就是复杂系统的涌现行为。