加法器

全加器

前提假设：


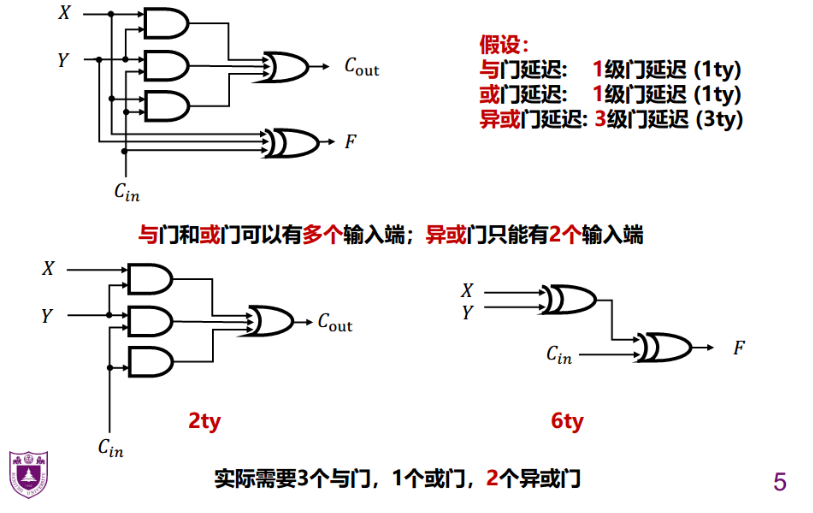
image.png

第一种

公式：

image.png

image.png

第二种

公式


image.png

其中，并非
的返回值为真，而是因为和前面的X与Y相配合，刚好形成了对应的结果


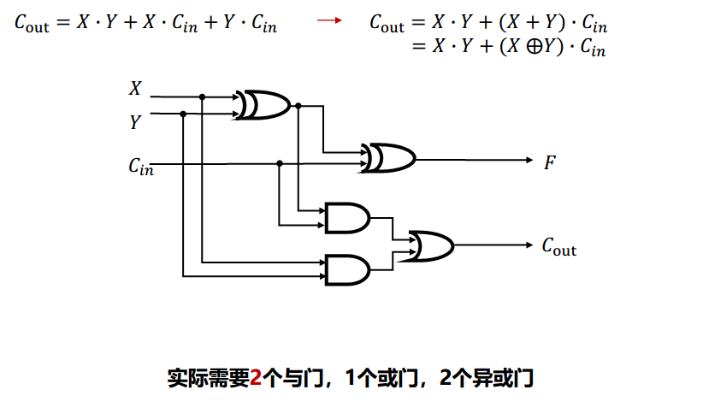
image.png
那么这种改善的好处是，减少了与门的使用

串行进位（行波进位）加法器

  • 1位加法：
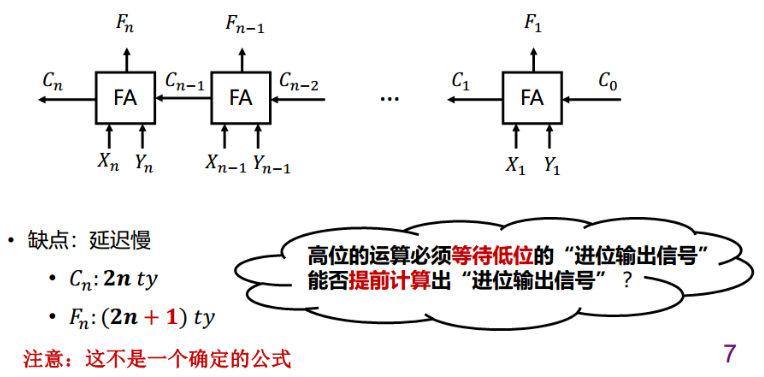
    image.png
  • 第i位加法：

image.png


image.png


Cn 是2n的延迟，原因是每个延迟为2：与操作+或操作
Fn是2n+1的延迟，原因是，



其中，

额外+3 是因为F产生的延迟。需要注意的是


因此，不会产生额外的延迟

全先行进位加法器

image.png


image.png

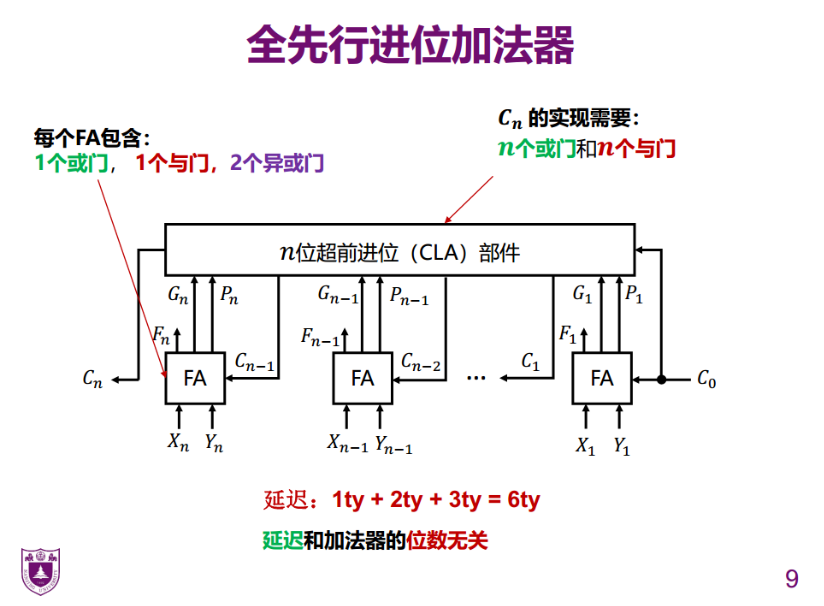
  • 1ty：代表的是生成信号和传播信号的生成
  • 2ty：代表的是第i个进位信号的生成：1延迟的与运算+1延迟的或运算【与运算和或运算可以接受任意个数的参数】
  • 3ty：代表的是第i个本位的生成：3延迟的或运算【和之前的1+2并行消耗，先计算X和Y的异或运算，经过3延迟后，C也得到了】+3延迟的或运算

部分先行进位加法器

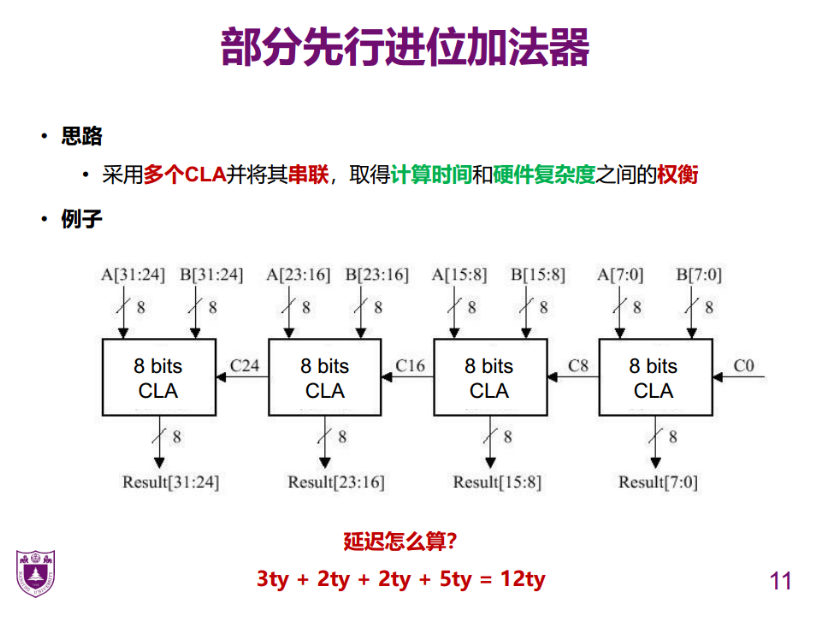
image.png

  • 3ty=2ty+1ty

在最开始时，

image.png此时的计算需要最初的1ty，之后，再根据计算公式可知需要2ty的延迟来生成
因此总延迟为3

  • 2ty 2ty 分别代表
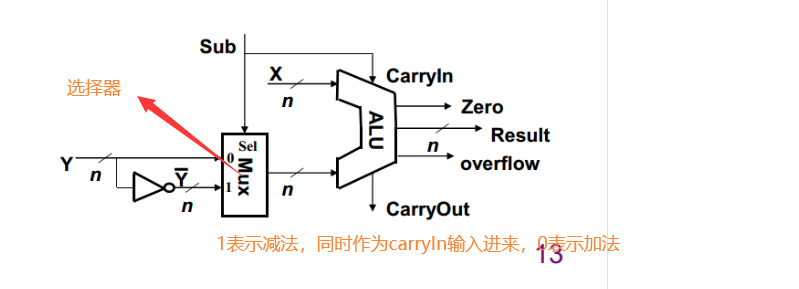
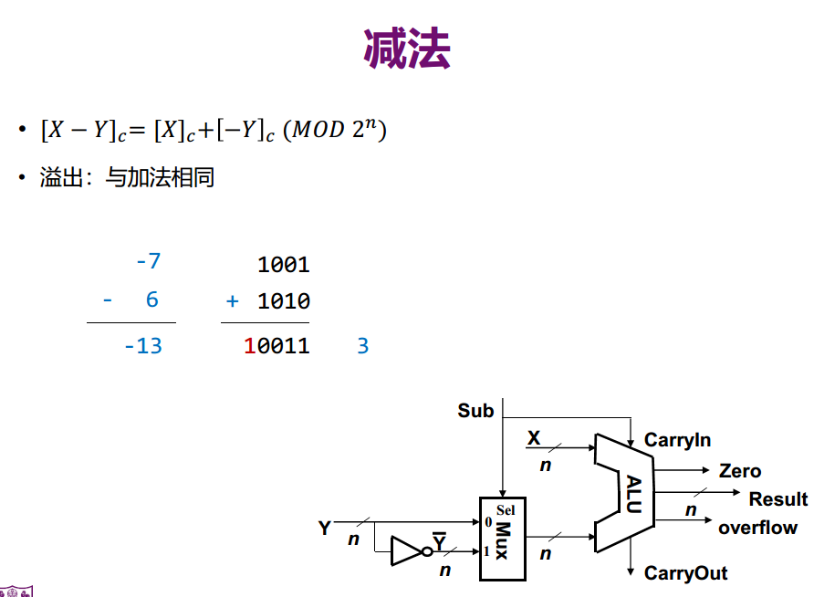
    image.png和
    的生成
  • 5ty = 3ty + 2ty 其中3ty代表的则是F的生成，2ty代表最后一次进位的生成

四则运算

加法

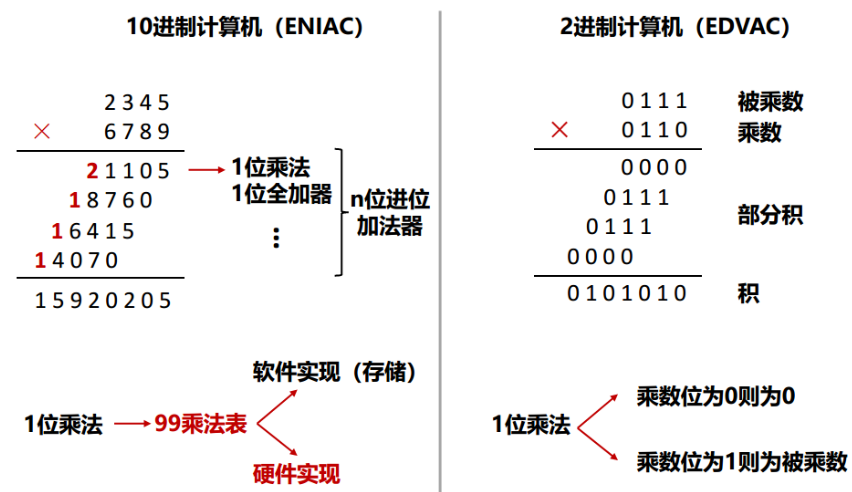
image.png


标注：此处的

单单第n位

减法

image.png

image.png

乘法

二进制乘法不需要乘法表进行存储。十分方便

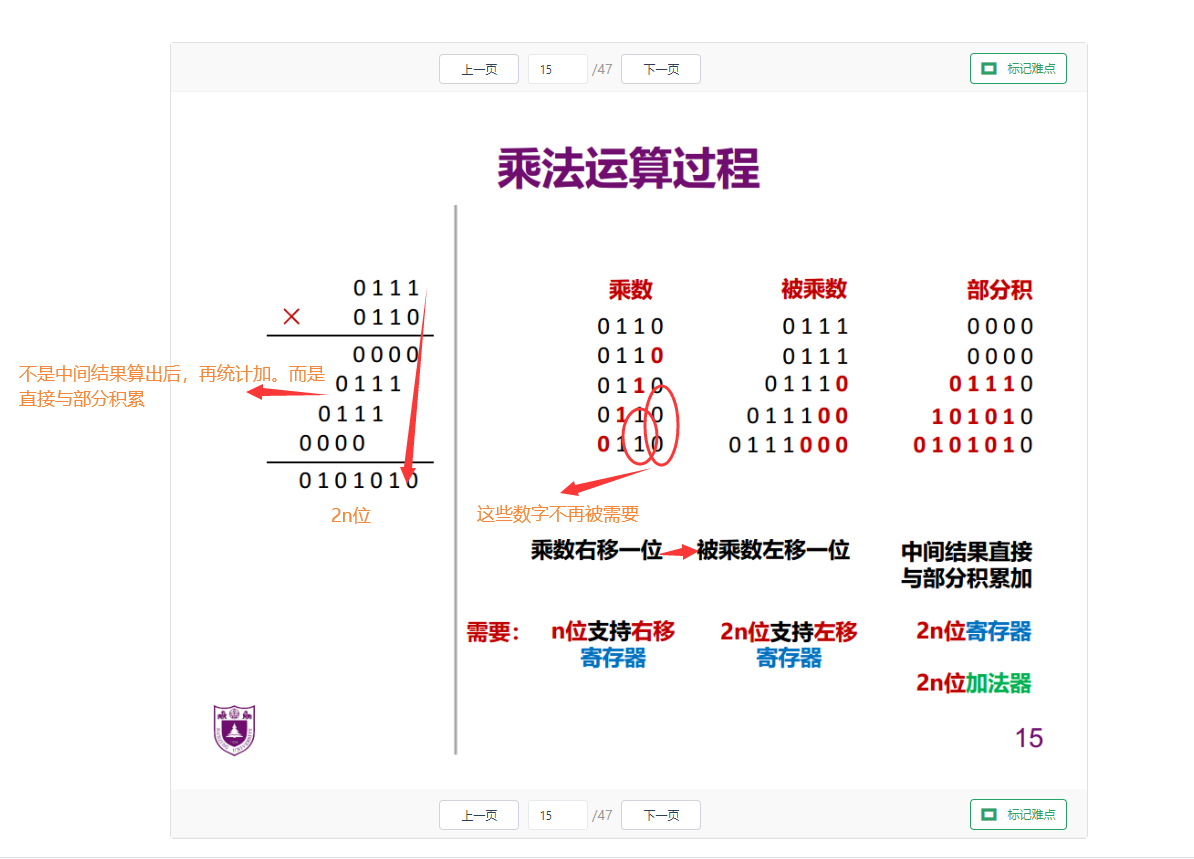
image.png

image.png

优化

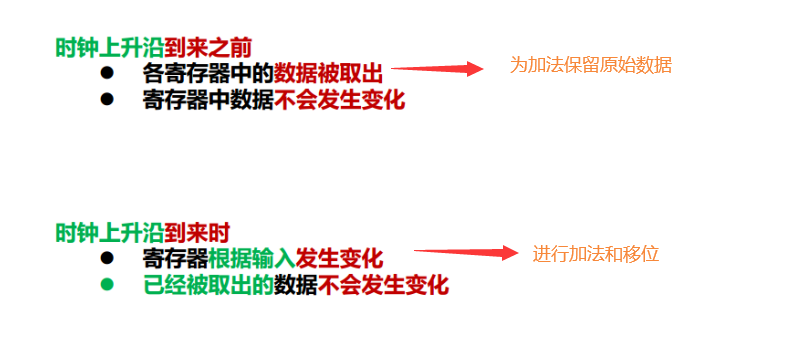
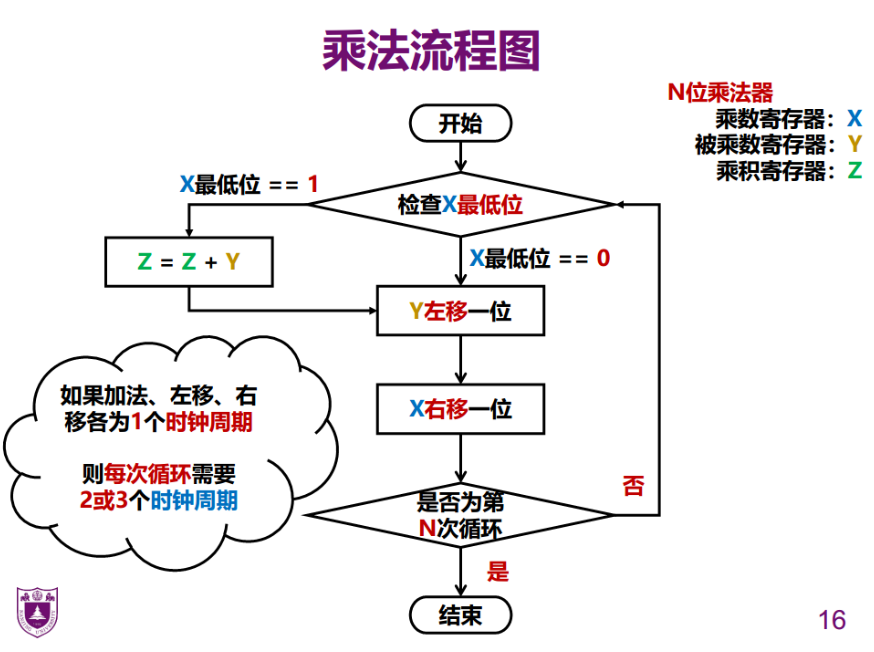
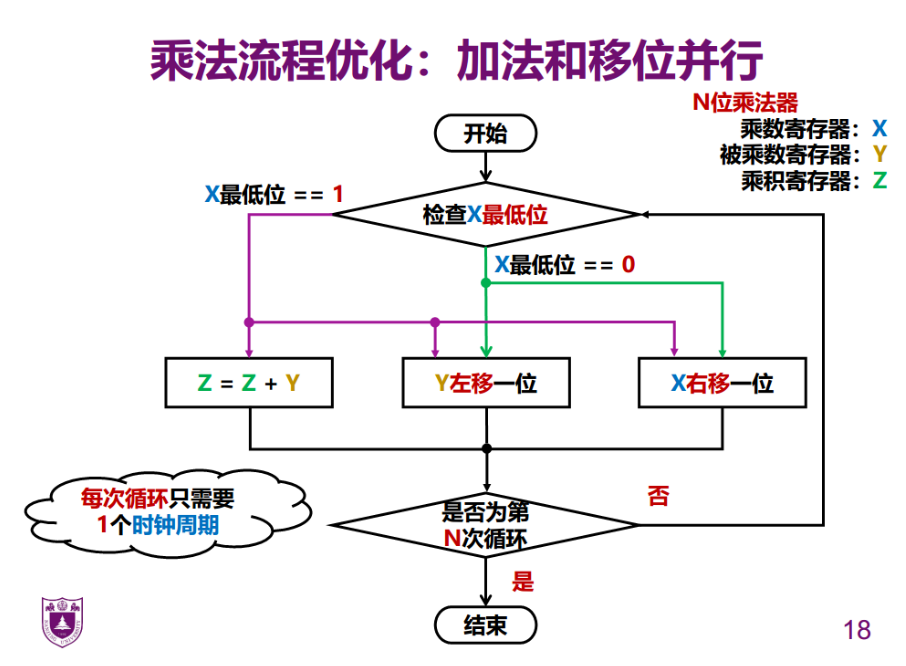
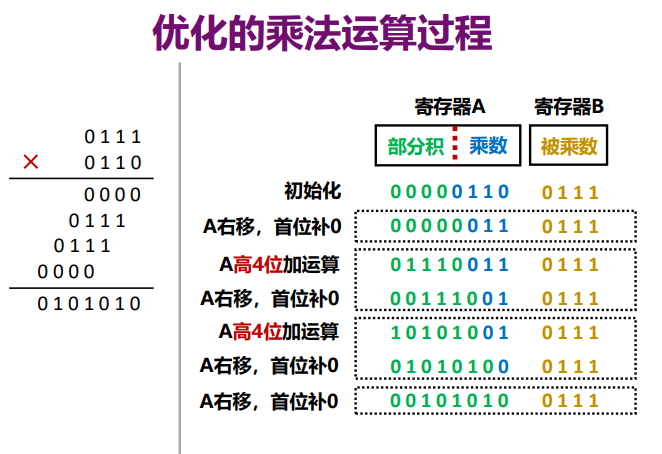
image.png


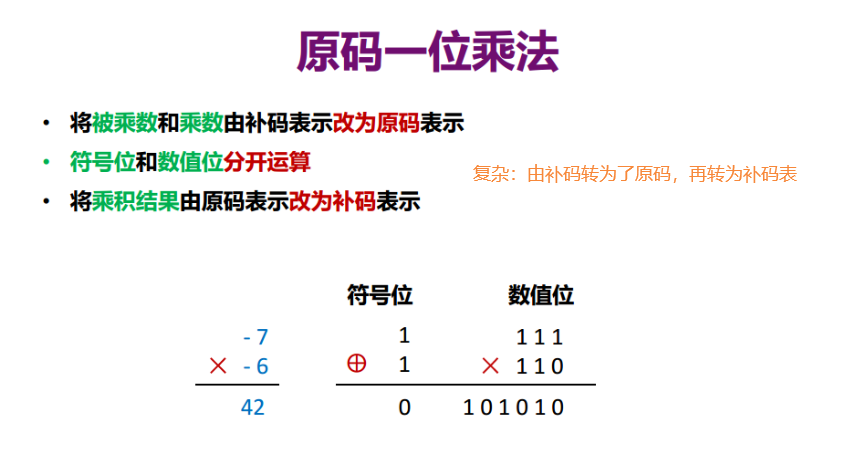
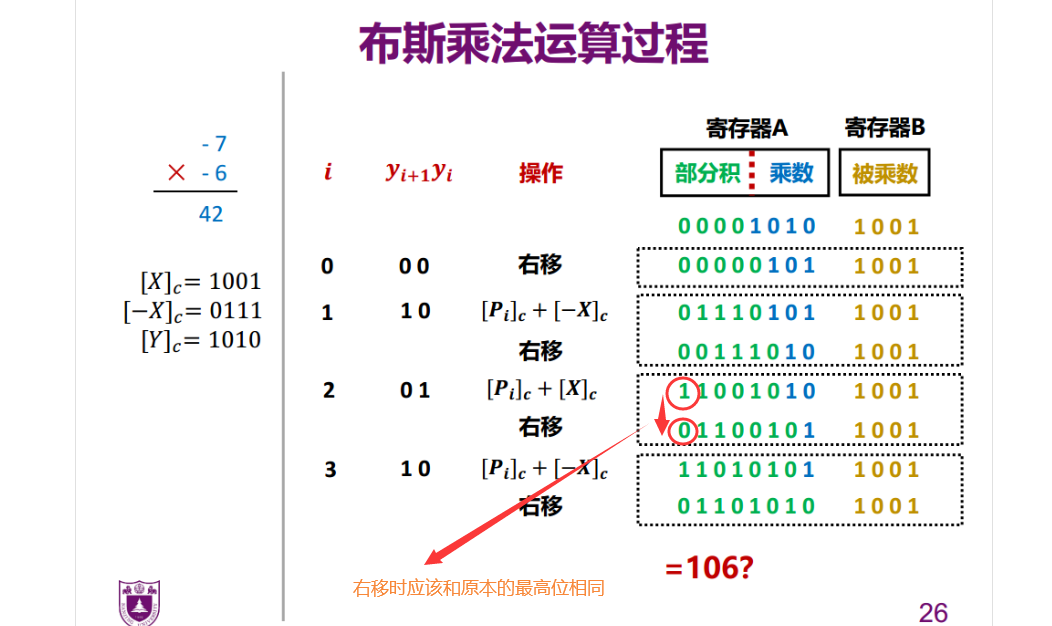
image.png


image.png


image.png

出错

  1. 原码一位乘法

image.png

image.png

除法

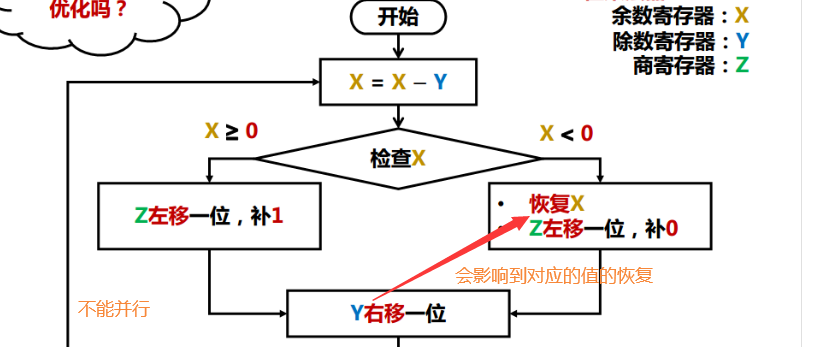
原码：恢复余数法

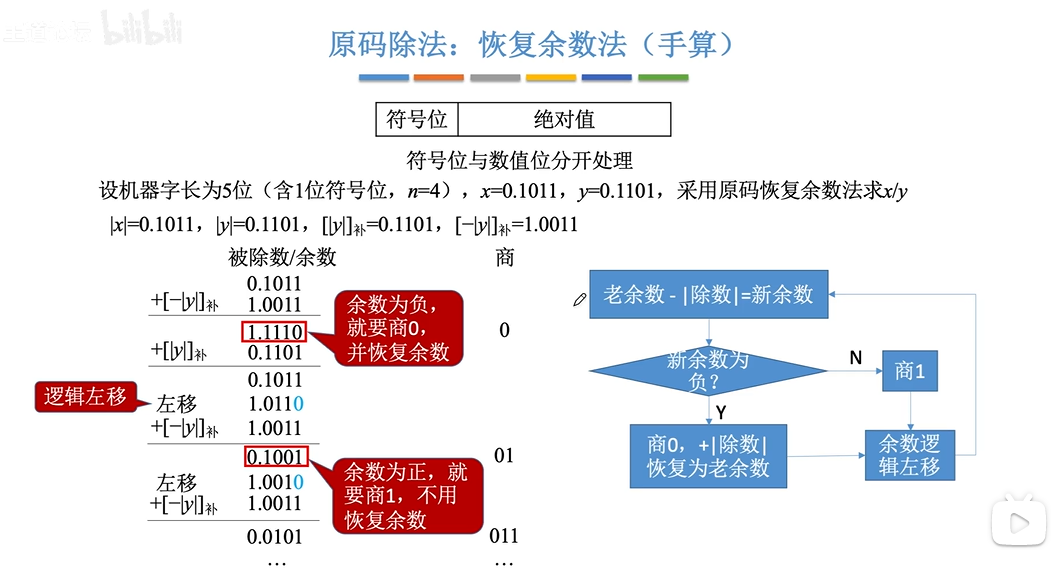
image.png
余数逻辑左移是为了实现错位相减。因为手算时实际上是除数右移，而我们规定除数不移动时，则是余数左移

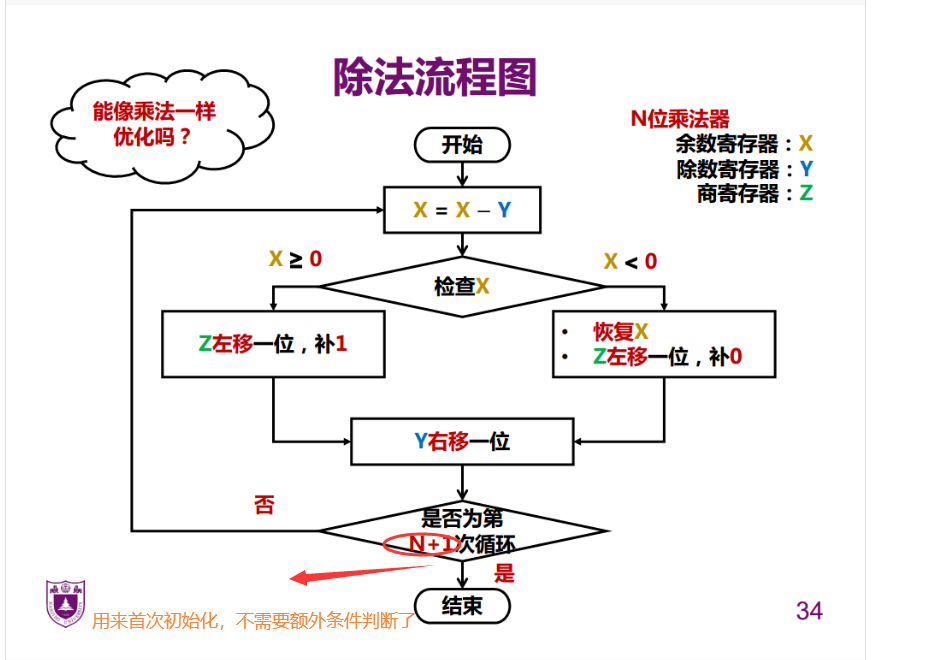
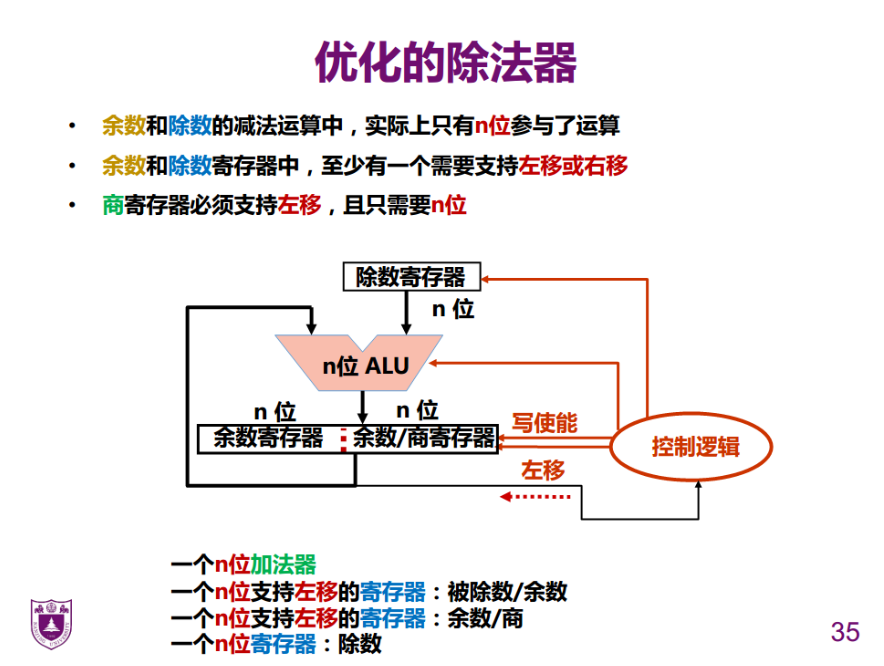
image.png

优化：并行+硬件的节省
并行：

image.png

原码：不恢复余数法

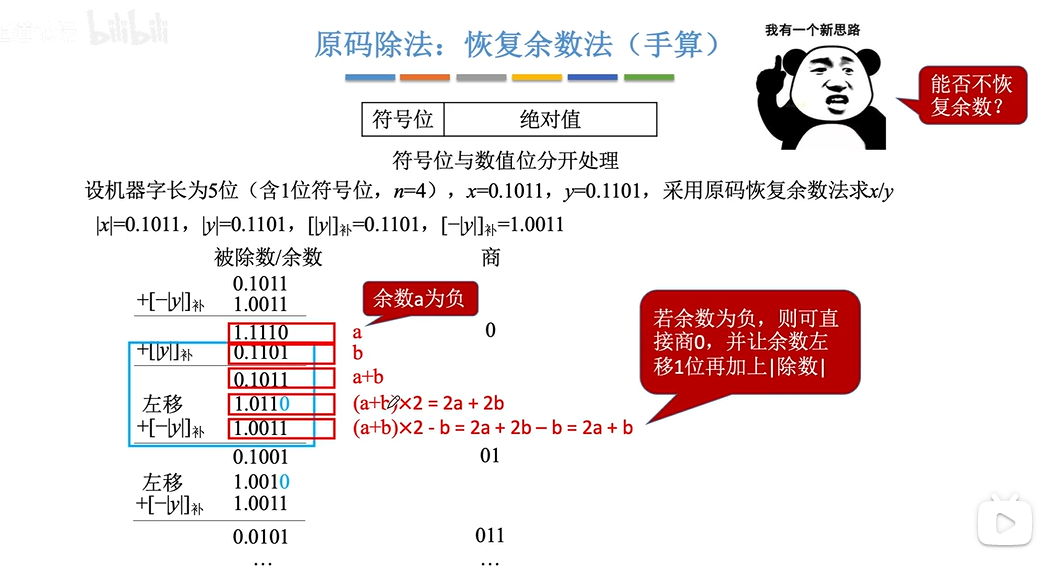
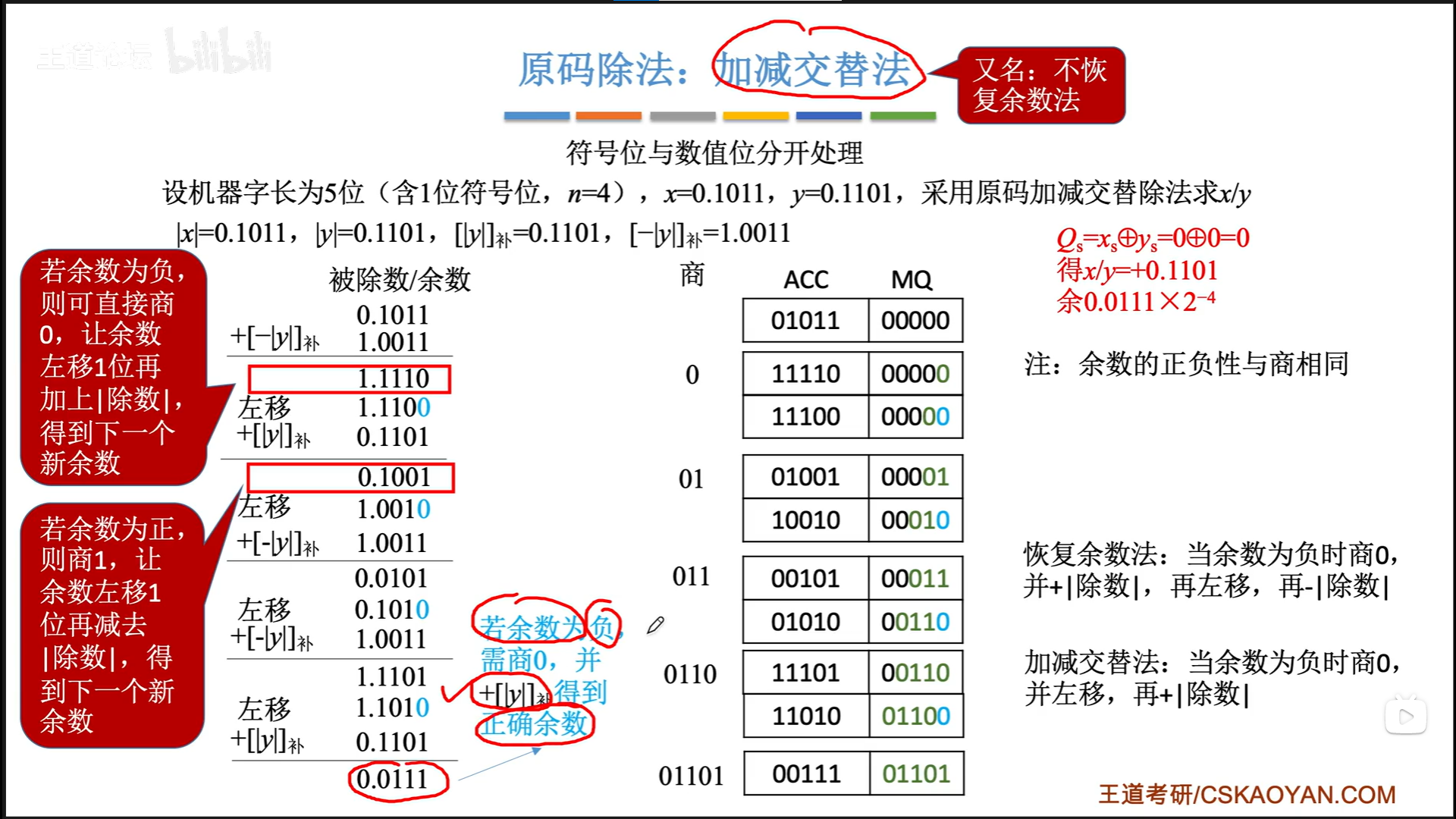
image.png


image.png
若最后一步余数为负数，仍然需要恢复为正确余数

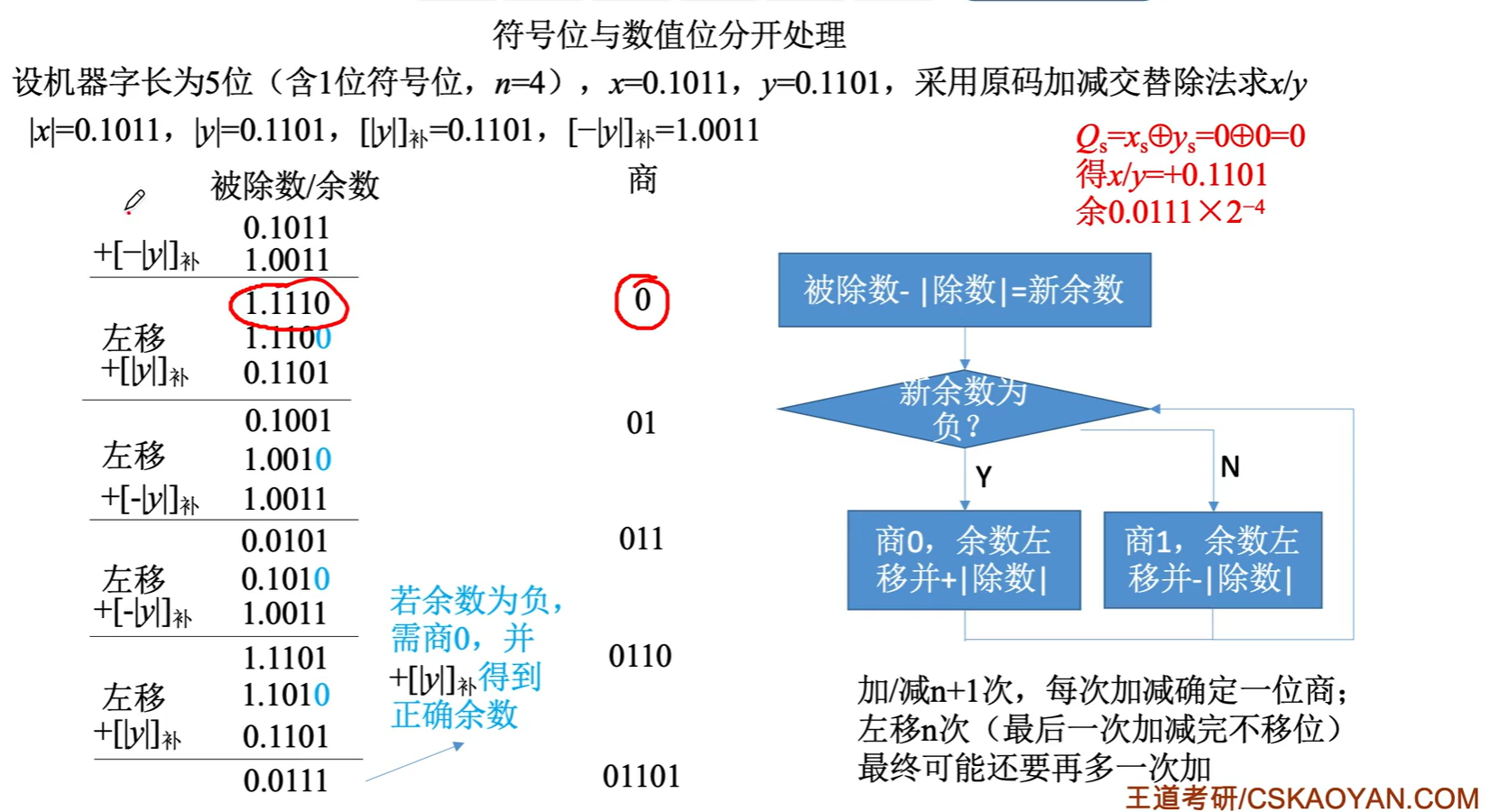
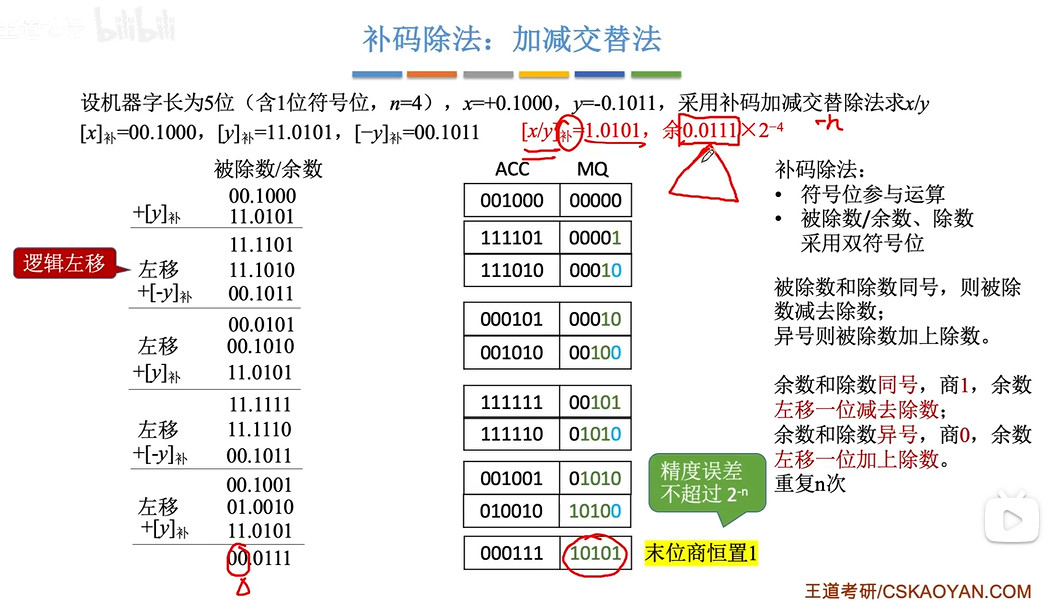
image.png

余数和被除数的符号相同

补码：不恢复余数法

余数和除数相减：

  • 如果余数和除数的符号相同：减法
  • 如果余数和除数的符号不同：加法
  1. 够减：余数和新余数的符号不能变
  2. 不够减：余数和新余数的符号改变

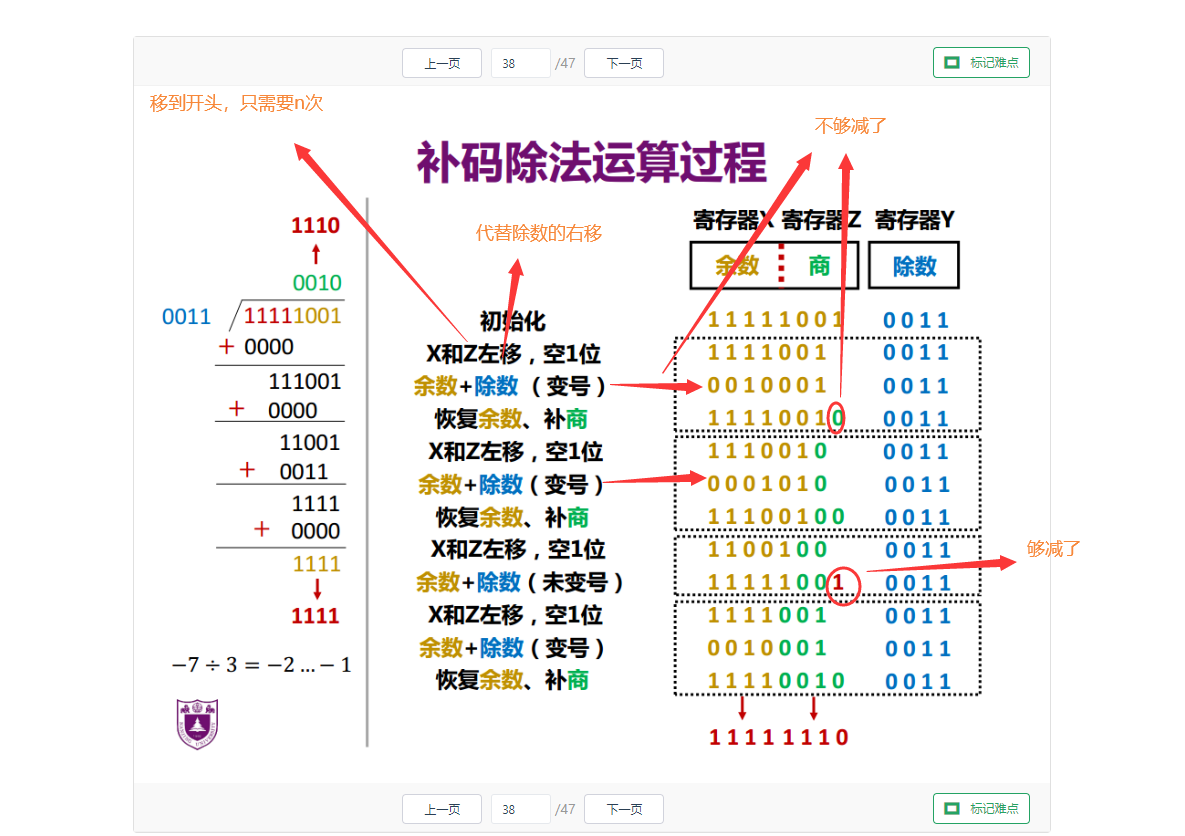
image.png


image.png

除法硬件改善

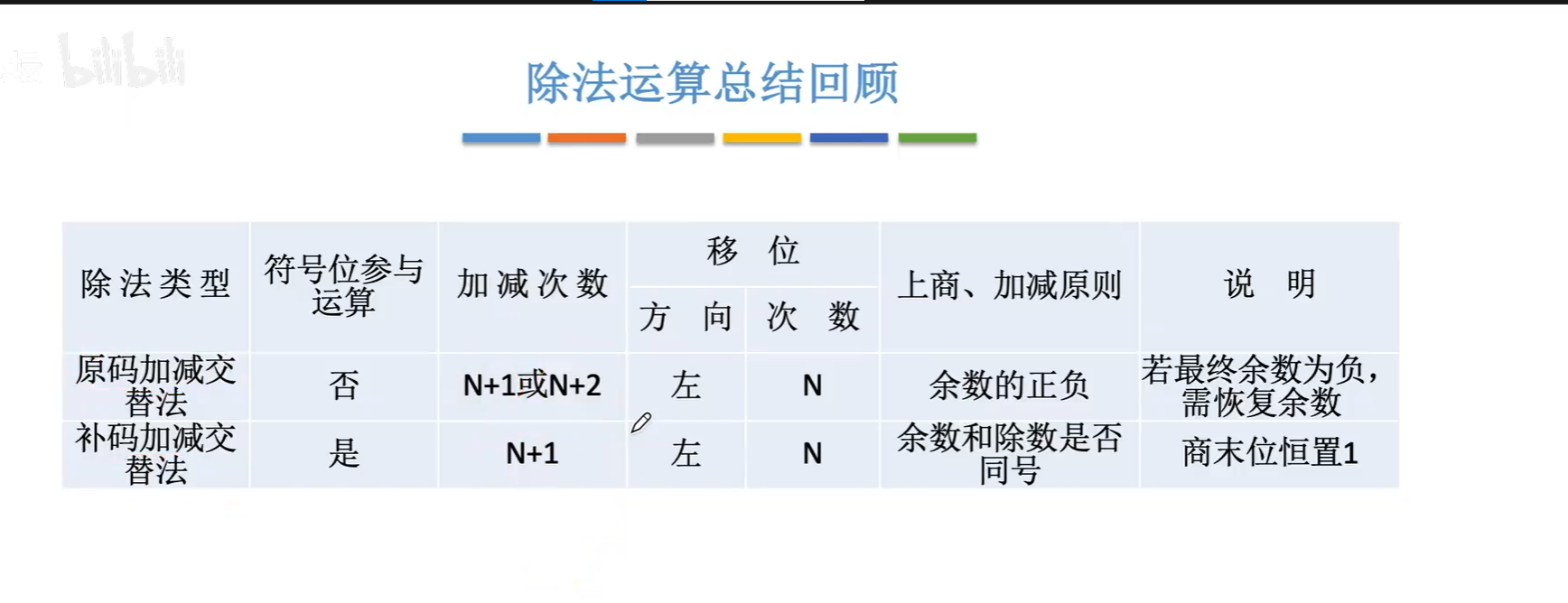
image.png

image.png
被除数移动了，除数就不需要移动了

除法运算总结

image.png

溢出

乘法溢出

image.png